8. Relationale Algebra

8.1. Einführung

■ Bisher
□ Relationenschemata mit Basisrelationen, die in der Datenbank gespeichert sind

■ Jetzt
□ „Abgeleitete“ Relationenschemata mit virtuellen Relationen, die aus den Basisrelationen berechnet werden
□ Definiert durch Anfragen
– Anfragesprache
□ Basisrelationen bleiben unverändert

8.1.1. Kriterien für Anfragesprachen

■ Ad-Hoc-Formulierung
□ Benutzer soll eine Anfrage formulieren können, ohne ein vollständiges Programm schreiben zu müssen.

■ Eingeschränktheit
□ Anfragesprache soll keine komplette Programmiersprache sein
– Aber: SQL Standard besteht aus >1300 Seiten…

■ Deskriptivität / Deklarativität
□ Benutzer soll formulieren „Was will ich haben?“ und nicht „Wie komme ich an das, was ich haben will?“

■ Optimierbarkeit
□ Sprache besteht aus wenigen Operationen
□ Optimierungsregeln für die Operatorenmenge

■ Effizienz
□ Jede einzelne Operation ist effizient ausführbar.
□ Im relationalen Modell hat jede Operation eine Komplexität ≤ O(n²)
– n = Anzahl der Tupel einer Relation

■ Abgeschlossenheit
□ Anfragen auf Relationen
□ Anfrageergebnis ist wiederum eine Relation und kann als Eingabe für die nächste Anfrage verwendet werden.

■ Mengenorientiertheit
□ Operationen auf Mengen von Daten
□ Nicht navigierend nur auf einzelnen Elementen („tuple-at-a-time“)

■ Adäquatheit
□ Alle Konstrukte des zugrundeliegenden Datenmodells werden unterstützt
□ Relationen, Attribute, Schlüssel, …

■ Vollständigkeit
□ Sprache muss mindestens die Anfragen einer Standardsprache (z.B. relationale Algebra) ausdrücken können.
□ Relationale Algebra dient als Vorgabe.

■ Sicherheit
□ Keine Anfrage, die syntaktisch korrekt ist, darf in eine Endlosschleife geraten oder ein unendliches Ergebnis liefern.

8.1.2. Anfragealgebra

■ Mathematik
□ Algebra: Definiert durch Wertebereich und auf diesem definierte Operatoren
□ Operand: Variablen oder Werte aus denen neue Werte konstruiert werden können
□ Operator: Symbole, die Prozeduren repräsentieren, die aus gegebenen Werten neue Werte produzieren

■ Für Datenbankanfragen
□ Inhalte der Datenbank (Relationen) sind Operanden
□ Operatoren definieren Funktionen zum Berechnen von Anfrageergebnissen
– Grundlegenden Dinge, die wir mit Relationen tun wollen.
□ Relationale Algebra (Relational Algebra, RA)
– Anfragesprache für das relationale Modell

8.1.3. Mengen vs. Multimengen

Relation: Menge von Tupeln
■ Datenbanktabelle: Multimenge von Tupeln
□ Engl: „bag“

■ Operatoren der relationalen Algebra: Operatoren auf Mengen

■ Operatoren auf DBMS: SQL Anfragen
□ Rel. DBMS speichern Multimengen

■ Motivation: Effizienzsteigerung
□ Beispiel:
– Vereinigung als Multimenge
– Vereinigung als Menge

8.2. Basisoperatoren

8.3. Klassifikation der Operatoren

■ Mengenoperatoren
□ Vereinigung, Schnittmenge, Differenz

■ Entfernende Operatoren
□ Selektion, Projektion

■ Kombinierende Operatoren
□ Kartesisches Produkt, Join, Joinvarianten

■ Umbenennung
□ Verändert nicht Tupel, sondern Schema

■ Ausdrücke der relationalen Algebra
□ Kombination von Operatoren und Operanden
□ „Anfragen“ (queries)

8.4. Vereinigung (union, \(\cup\))

■ Sammelt Elemente (Tupel) zweier Relationen unter einem gemeinsamen Schema auf.
□ R ∪ S := {t | t \(\in\) R \(\vee\) t \(\in\) S}

■ Attributmengen beider Relationen müssen identisch sein.
□ Namen, Typen und Reihenfolge
□ Zur Not: Umbenennung

■ Ein Element ist nur einmal in (R ∪ S) vertreten, auch wenn es jeweils einmal in R und S auftaucht.
□ Duplikatentfernung

8.5. Beispiel für Mengenoperatoren

\(R\)

Name	Adresse	Geschlecht	Geburt
Carrie Fisher	123 Maple St., Hollywood	F	9/9/99
Mark Hamill	456 Oak. Rd., Brentwood	M	8/8/88

\(S\)

Name	Adresse	Geschlecht	Geburt
Carrie Fisher	123 Maple St., Hollywood	F	9/9/99
Harrison Ford	789 Palm Dr., Beverly Hills	M	7/7/77

\(R \cup S\)

Name	Adresse	Geschlecht	Geburt
Carrie Fisher	123 Maple St., Hollywood	F	9/9/99
Mark Hamill	456 Oak. Rd., Brentwood	M	8/8/88
Harrison Ford	789 Palm Dr., Beverly Hills	M	7/7/77

8.6. Differenz (difference, ―, \)

■ Differenz R − S eliminiert die Tupel aus der ersten Relation, die auch in der zweiten Relation vorkommen.
□ R − S := {t | t \(\in\) R \(\wedge\) t \(\notin\) S}

■ Achtung: Schemata von R und S müssen gleich sein.

■ Achtung: R − S ≠ S − R
□ D.h. Kommuntativität gilt nicht

8.7. Beispiel für Mengenoperatoren

\(R\)

Name	Adresse	Geschlecht	Geburt
Carrie Fisher	123 Maple St., Hollywood	F	9/9/99
Mark Hamill	456 Oak. Rd., Brentwood	M	8/8/88

\(S\)

Name	Adresse	Geschlecht	Geburt
Carrie Fisher	123 Maple St., Hollywood	F	9/9/99
Harrison Ford	789 Palm Dr., Beverly Hills	M	7/7/77

\(R-S\)

Name	Adresse	Geschlecht	Geburt
Mark Hamill	456 Oak. Rd., Brentwood	M	8/8/88

8.8. Schnittmenge (intersection, \(\cap\))

Schnittmenge R \(\cap\) S ergibt die Tupel, die in beiden Relationen gemeinsam vorkommen.

■ R \(\cap\) S := {t | t \(\in\) R \(\wedge\) t \(\in\) S}

■ Anmerkung: Schnittmenge ist „überflüssig“. Warum?
□ R \(\cap\) S = R − (R − S)
= S − (S − R)

8.9. Beispiel für Mengenoperatoren

\(R\)

Name	Adresse	Geschlecht	Geburt
Carrie Fisher	123 Maple St., Hollywood	F	9/9/99
Mark Hamill	456 Oak. Rd., Brentwood	M	8/8/88

\(S\)

Name	Adresse	Geschlecht	Geburt
Carrie Fisher	123 Maple St., Hollywood	F	9/9/99
Harrison Ford	789 Palm Dr., Beverly Hills	M	7/7/77

\(R\cap S\)

Name	Adresse	Geschlecht	Geburt
Carrie Fisher	123 Maple St., Hollywood	F	9/9/99

8.10. Projektion (projection, \(\pi\))

■ Unärer Operator

■ Erzeugt neue Relation mit einer Teilmenge der ursprünglichen Attribute

■ \(\pi_{A1,A2,…,Ak}\)® ist eine Relation
□ mit den Attributen A1,A2,…,Ak
□ Üblicherweise in der aufgelisteten Reihenfolge

■ Achtung: Es können Duplikate entstehen, die implizit entfernt werden.

8.11. Projektion – Beispiel

Film

Titel	Jahr	Länge	inFarbe	Studio	ProduzentID
Total Recall	1990	113	True	Fox	12345
Basic Instinct	1992	127	True	Disney	67890
Dead Man	1995	121	False	Paramount	99999

\(\pi_{Titel,Jahr,Länge}\)(Film)

Titel	Jahr	Länge
Total Recall	1990	113
Basic Instinct	1992	127
Dead Man	1995	121

\(\pi_{inFarbe}\)(Film)

inFarbe
True
False

8.12. Erweiterte Projektion

■ Motivation: Dem Projektionsoperator mehr Fähigkeiten geben

■ Vorher: \(\pi_{L}\)® wobei L eine Attributliste ist

■ Nun: Ein Element von L ist eines dieser drei Ausdrücke

1. Ein Attribut von R (wie zuvor)
   

2. Ein Ausdruck A→B wobei A ein Attribut in R ist und B ein neuer Name ist (Umbennennung).
   

3. Ein Ausdruck e→C, wobei e ein Ausdruck mit Konstanten, arithmetischen Operatoren, Attributen von R und String-Operationen ist, und C ein neuer Name ist.
   

4. A1 + A2 → Summe
   

5. Vorname || ` ` || Nachname → Name

8.13. Selektion (selection, \(\sigma\))

■ Unärer Operator

■ Erzeugt neue Relation mit gleichem Schema aber einer Teilmenge der Tupel.

■ Nur Tupel, die der Selektionsbedingung C (condition) entsprechen.
□ Selektionsbedingung wie aus Programmiersprachen
□ Operanden der Selektionsbedingung sind nur Konstanten oder Attribute von R.
– const = const (eigentlich unnötig)
– attr = const (typische Selektion)
– attr = attr (Join Bedingung)
□ Weitere Vergleiche: <, >, ≤, \(\ge\), <>
□ Kombination durch AND, OR und NOT

■ Prüfe Bedingung für jedes Tupel

Achtung Selektion \(\neq\) SELECT

8.14. Selektion – Beispiel

Film

Titel	Jahr	Länge	inFarbe	Studio	ProduzentID
Total Recall	1990	113	True	Fox	12345
Basic Instinct	1992	127	True	Disney	67890
Dead Man	1995	90	False	Paramount	99999

\(\sigma_{Länge\geq100}\)(Film)

Titel	Jahr	Länge	inFarbe	Studio	ProduzentID
Total Recall	1990	113	True	Fox	12345
Basic Instinct	1992	127	True	Disney	67890

\(\sigma_{Länge\geq100 AND Studio='Fox'}\)(Film)

Titel	Jahr	Länge	inFarbe	Studio	ProduzentID
Total Recall	1990	113	True	Fox	12345

8.15. Kartesisches Produkt (Cartesian product, cross product \(\times\))

■ Binärer Operator

■ Auch: Kreuzprodukt oder Produkt

■ Auch: R * S statt R \(\times\) S

■ Kreuzprodukt zweier Relationen R und S ist die Menge aller Tupel, die man erhält, wenn man jedes Tupel aus R mit jedem Tupel aus S „paart“.

■ Schema hat ein Attribut für jedes Attribut aus R und S
□ Achtung: Bei Namensgleichheit wird kein Attribut ausgelassen
□ Stattdessen: Umbenennen

8.16. Kartesisches Produkt – Beispiel

\(R\)

A	B
1	2
3	4

\(S\)

B	C	D
2	5	6
4	7	8
9	10	11

\(R \times S\)

A	R.B	S.B	C	D
1	2	2	5	6
1	2	4	7	8
1	2	9	10	11
3	4	2	5	6
3	4	4	7	8
3	4	9	10	11

8.17. Der Join – Operatorfamilie

■ Natürlicher Join (natural join)

■ Theta-Join

■ Equi-Join

■ Semi-Join und Anti-Join

■ Left-outer Join und Right-outer Join

■ Full-outer Join

8.17.1. Natürlicher Join (natural join, ⋈)

■ Binärer Operator

■ Motivation: Statt im Kreuzprodukt alle Paare zu bilden, sollen nur die Tupelpaare gebildet werden, deren Tupel „irgendwie“ übereinstimmen.
□ Auch: „Verbund“
□ Beim natürlichen Join: Übereinstimmung in allen gemeinsamen Attributen.
□ Gegebenenfalls Umbenennung
□ Schema: Vereinigung der beiden Attributmengen

■ Notation: r[A] sei Projektion der Tupels r auf Attribut A

■ Seien A1,…,Ak die gemeinsamen Attribute von R und S

■ R ⋈ S = {r \(\cup\) s | r\(\in\)R \(\wedge\) s\(\in\)S \(\wedge\) r[A1]=s[A1] \(\wedge\) … \(\wedge\) r[Ak]=s[Ak] }

■ Alternative, üblichere Definition
□ R ⋈ S = s r[A1]=s[A1] \(\wedge\) … \(\wedge\) r[Ak]=s[Ak](R × S)
□ Achtung: Eigentlich noch ordentlich projizieren

8.17.2. Natürlicher Join – Beispiel

\(R\)

A	B
1	2
3	4

\(S\)

B	C	D
2	5	6
4	7	8
9	10	11

\(R ⋈ S\)

A	B	C	D
1	2	5	6
3	4	7	8

\(R \times S\)

A	R.B	S.B	C	D
1	2	2	5	6
1	2	4	7	8
1	2	9	10	11
3	4	2	5	6
3	4	4	7	8
3	4	9	10	11

\(R\)

A	B	C
1	2	3
6	7	8
9	7	8

\(S\)

B	C	D
2	5	6
2	3	5
7	8	10

\(R ⋈ S\)

A	B	C	D
1	2	3	5
6	7	8	10
9	7	8	10

■ Anmerkungen
□ Mehr als ein gemeinsames Attribut
□ Tupel werden mit mehr als einem Partner verknüpft

8.17.3. Theta-Join (theta-join, \(⋈_\theta\))

■ Verallgemeinerung des natürlichen Joins

■ Verknüpfungsbedingung kann selbst gestaltet werden

■ Konstruktion des Ergebnisses:
□ Bilde Kreuzprodukt der beiden Relationen
□ Selektiere mittels der gegebenen Joinbedingung
□ Also: R ⋈\(A_\theta\) B S = s \(A_\theta\) B (R \(\times\) S)
□ \(\theta\) ∈ {=, <, >, ≤, ≥, ≠}
□ A ist Attribut in R; B ist Attribut in S

■ Schema: Wie beim Kreuzprodukt

■ Equi-Join ist ein Spezialfall des Theta-Joins mit Operator „=“

■ Natural Join ist ein Spezialfall des Theta-Joins
□ Aber: Schema des Ergebnisses sieht anders aus.
□ R(A,B,C) ⋈ S(B,C,D) = \(\rho_{T(A,B,C,D)}\)(\(\pi_{A,R.B,R.C,D}\)(\(\sigma_{(R.B=S.B AND R.C = S.C)}\) (\(R \times S\))))
->Umbenennung

8.17.4. Theta-Join – Beispiel

\(R\)

A	B	C
1	2	3
6	7	8
9	7	8

\(S\)

B	C	D
2	5	6
2	3	5
7	8	10

\(R ⋈_{A<D}S\)

A	R.B	R.C	S.B	S.C	D
1	2	3	2	5	6
1	2	3	2	3	5
1	2	3	7	8	10
6	7	8	7	8	10
9	7	8	7	8	10

\(R ⋈_{A<D \wedge R.B \neq S.B}S\)

A	R.B	R.C	S.B	S.C	D
1	2	3	7	8	10

8.17.5. Komplexe Ausdrücke

■ Idee: Kombination (Schachtelung) von Ausdrücken zur Formulierung komplexer Anfragen.
□ Abgeschlossenheit der relationalen Algebra
– Output eines Ausdrucks ist immer eine Relation.

□ Darstellung
– Als geschachtelter Ausdruck mittels Klammerung
– Als Baum

Film

Titel	Jahr	Länge	Typ	StudioName
Total Recall	1990	113	Farbe	Fox
Basic Instinct	1992	127	Farbe	Disney
Dead Man	1995	90	s/w	Paramount

■ Gesucht: Titel und Jahr von Filmen, die von Fox produziert wurden und mindestens 100 Minuten lang sind.
□ Suche alle Filme von Fox
□ Suche alle Filme mit mindestens 100 Minuten
□ Bilde die Schnittmenge der beiden Zwischenergebnisse
□ Projiziere die Relation auf die Attribute Titel und Jahr.
□ \(\rho_{Titel,Jahr}\)(\(\sigma_{Länge≥100}\)(Film) \(\cap\) \(\sigma_{StudioName=‚Fox‘}\)(Film))
□ Alternative: \(\pi_{Titel,Jahr}\)(\(\sigma_{Länge≥100 AND StudioName=‚Fox‘}\)(Film))
– U.v.a.m.

8.17.6. Komplexe Ausdrücke – Beispiel

■\(\rho_{Titel,Jahr}\)(\(\sigma_{Länge≥100(Film)}\) \(\cap\) \(\sigma_{StudioName=‚Fox‘}\)(Film))

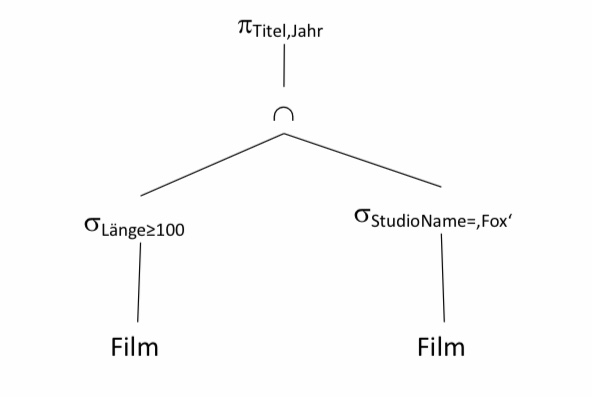
■ Alternative: \(\rho_{Titel,Jahr}\)(\(\sigma_{Länge≥100 AND StudioName=‚Fox‘}\)(Film))

8.17.7. Komplexe Ausdrücke – Beispiel

Film

Titel	Jahr	Länge	Typ	StudioName
Total Recall	1990	113	Farbe	Fox
Basic Instinct	1992	127	Farbe	Disney
Dead Man	1995	90	s/w	Paramount

Rolle

Titel	Jahr	SchauspName
Total Recall	1990	Sharon Stone
Basic Instinct	1992	Sharon Stone
Total Recall	1990	Arnold
Dead Man	1995	Johnny Depp

■ Gesucht: Namen aller Schauspieler, die in Filmen spielten, die mindestens 100 Minuten lang sind.
□ Verjoine beide Relationen (natürlicher Join)
□ Selektiere Filme, die mindestens 100 Minuten lang sind.
□ \(\rho_{SchauspName}\)(\(\sigma_{Länge≥100}\)(Film ⋈ Rolle))

■ Stud(Matrikel, Name, Semester)
■ Prof(ProfName, Fachgebiet, GebJahr)
■ VL(VL_ID, Titel, Saal)
■ Lehrt(ProfName, VL_ID)
■ Hört(Matrikel,VL_ID)
■ Gesucht: Unterschiedliche Semester aller Studierenden, die eine Vorlesung eines Professors des Jahrgangs 1960 in Hörsaal 1 hören.
■ \(\rho_{Sem}\)(((\(\sigma_{Saal=1}\)(((\(\sigma_{GebJahr = 1960}\)(Professor))⋈Lehrt)⋈VL)⋈Hört)⋈Stud))

8.17.8. Umbenennung (rename, \(\rho\))

■ Unärer Operator

■ Motivation: Zur Kontrolle der Schemata und einfacheren Verknüpfungen
□ \(\rho_{S(A1,…,An)}\)®
– Benennt Relation R in S um
– Benennt die Attribute der neuen Relation A1,…,An
□ \(\rho_{S(R)}\) benennt nur Relation um.
■ Durch Umbenennung ermöglicht
□ Mengenoperationen
– Nur möglich bei gleichen Schemata
□ Joins, wo bisher kartesische Produkte ausgeführt wurde
– Unterschiedliche Attribute werden gleich benannt.
□ Kartesische Produkte, wo bisher Joins ausgeführt wurden
– Gleiche Attribute werden unterschiedlich genannt.

8.17.9. Umbenennung – Beispiel

\(R\)

A	B
1	2
3	4

\(S\)

B	C	D
2	5	6
4	7	8
9	10	11

\(R \times \rho_{s(X,C,D)}(S)\)

A	B	X	C	D
1	2	2	5	6
1	2	4	7	8
1	2	9	10	11
3	4	2	5	6
3	4	4	7	8
3	4	9	10	11

■ Alternativer Ausdruck: \(\rho_{S(A,B,X,C,D)}\)(R \(\times\) S)

8.17.10. Unabhängigkeit und Vollständigkeit

Minimale Relationenalgebra:
□ π, σ, \(\times\) , −, ∪ (und r)
■ Unabhängig:
□ Kein Operator kann weggelassen werden ohne Vollständigkeit zu verlieren.

■ Natural Join, Join und Schnittmenge sind redundant
□ R \(\cap\) S = R − (R − S)
□ R ⋈C S = \(\sigma_C\)(R \(\times\) S)
□ R ⋈ S = \(\pi_{L}\)(\(\sigma_{R.A1=S.A1 AND … AND R.An=S.An}\)(R \(\times\) S))

8.18. Vorschau zu Optimierung

■ Beispiele für algebraische Regeln zur Transformation
□ R ⋈ S = S ⋈ R
□ (R ⋈ S) ⋈ T = R ⋈ (S ⋈ T)
□ \(\rho_{Y}(\rho_{X}(R)) = \rho_{Y}(R)\)
– Falls Y ⊆ X
□ \(\sigma_{A=a}(\sigma_{B=b}(R))= \sigma_{B=b}(\sigma_{A=a}(R)) [ = \sigma_{B=b\wedge A=a}(R) ]\)
□ \(\pi_{X}(\sigma_{A=a}(R)) = \sigma_{A=a}(\pi_{X}(R))\)
– Falls A ⊆ X
□ \(\sigma_{A=a}(R ∪ S) = \sigma_{A=a}(R) ∪ \sigma_{A=a}(S)\)
■ Jeweils: Welche Seite ist besser?

8.19. Operatoren auf Multimengen

8.19.1. Motivation

Mengen sind ein natürliches Konstrukt
□ Keine Duplikate

■ Kommerzielle DBMS basieren fast nie nur auf Mengen
□ Sondern erlauben Multimengen
□ D.h. Duplikate sind erlaubt

■ Multimenge
□ bag, multiset

A	B
1	2
3	4
1	2
1	2

Multimenge
Reihenfolge ist weiter unwichtig

8.19.2. Effizienz durch Multimengen

■ Bei Vereinigung
□ Direkt „aneinanderhängen“

■ Bei Projektion
□ Einfach Attributwerte „abschneiden“

■ Nach Duplikaten suchen
□ Jedes Tupel im Ergebnis mit jedem anderen vergleichen
□ O(n²)

■ Effizienter nach Duplikaten suchen
□ Nach allen Attributen zugleich sortieren: O(n log n)

■ Bei Aggregation
□ Duplikateliminierung sogar schädlich bzw. unintuitiv
□ AVG(A) = ?

Projektion auf (A,B)

A	B	C
1	2	5
3	4	6
1	2	7
1	2	8

8.19.3. Vereinigung auf Multimengen

Sei R eine Multimenge
□ Tupel t erscheine n-mal in R.

■ Sei S eine Multimenge
□ Tupel t erscheine m-mal in S.
■ Tupel t erscheint in R \(\cup\) S
□ (n+m) mal.

\(R\)

A	B
1	2
3	4
1	2
1	2

\(S\)

A	B
1	2
3	4
3	4
5	6

\(R \cup S\)

A	B
1	2
3	4
1	2
1	2
1	2
3	4
3	4
5	6

8.19.4. Schnittmenge auf Multimengen

■ Sei R eine Multimenge
□ Tupel t erscheine n-mal in R.

■ Sei S eine Multimenge
□ Tupel t erscheine m-mal in S.

■ Tupel t erscheint in R \(\cap\) S
□ min(n,m) mal.

\(R\)

A	B
1	2
3	4
1	2
3	4
1	2

\(S\)

A	B
1	2
3	4
3	4
5	6

\(R \cap S\)

A	B
1	2
3	4
3	4

8.20. Differenz auf Multimengen

■ Sei R eine Multimenge
□ Tupel t erscheine n-mal in R.

■ Sei S eine Multimenge
□ Tupel t erscheine m-mal in S.

■ Tupel t erscheint in R − S
□ max(0, n−m) mal.
□ Falls t öfter in R als in S vorkommt, bleiben n−m t übrig.
□ Falls t öfter in S als in R vorkommt, bleibt kein t übrig.
□ Jedes Vorkommen von t in S eliminiert ein t in R.

\(R\)

A	B
1	2
3	4
1	2
1	2

\(S\)

A	B
1	2
3	4
3	4
5	6

\(R-S\)

A	B
1	2
1	2

\(S-R\)

A	B
3	4
5	6

8.20.1. Projektion und Selektion auf Multimengen

■ Projektion
□ Bei der Projektion können neue Duplikate entstehen.
□ Diese werden nicht entfernt

■ Selektion
□ Selektionsbedingung auf jedes Tupel einzeln und unabhängig anwenden
□ Schon vorhandene Duplikate bleiben erhalten
– Sofern sie beide selektiert bleiben

\(R\)

A	B	C
1	2	5
3	4	6
1	2	7
1	2	7

\(\pi_{A,B}(R)\)

A	B
1	2
3	4
1	2
1	2

\(\sigma_{C\geq6}(R)\)

A	B	C
1	2	5
3	4	6
1	2	7
1	2	7

8.20.2. Kreuzprodukt auf Multimengen

Sei R eine Multimenge
□ Tupel t erscheine n-mal in R.
■ Sei S eine Multimenge
□ Tupel u erscheine m-mal in S.
■ Das Tupel tu erscheint in R \(\times\) S n·m-mal.

\(R\)

A	B
1	2
1	2

\(S\)

B	C
2	3
4	5
4	5

\(R \times S\)

A	R.B	S.B	C
1	2	2	3
1	2	2	3
1	2	4	5
1	2	4	5
1	2	4	5
1	2	4	5

8.20.3. Joins auf Multimengen

■ Keine Überraschungen

\(R\)

A	B
1	2
1	2

\(S\)

B	C
2	3
4	5
4	5

\(R⋈S\)

A	B	C
1	2	3
1	2	3

\(R⋈_{R.B<S.B}S\)

A	R.B	S.B	C
1	2	4	5
1	2	4	5
1	2	4	5
1	2	4	5

8.21. Erweiterte Operatoren

8.22. Überblick über Erweiterungen

Duplikateliminierung
■ Aggregation
■ Gruppierung
■ Sortierung
■ Outer Join
■ Outer Union
■ Semijoin
■ (Division)

8.22.1. Duplikateliminierung (duplicate elimination, \(\delta\))

■ Wandelt eine Multimenge in eine Menge um.
□ Durch Löschen aller Kopien von Tupeln
□ \(\delta\)®
– Strenggenommen unnötig: Mengensemantik der relationalen Algebra

\(R\)

A	B	C
1	2	a
3	4	b
1	2	c
1	2	d

\(\delta(\pi_{A,B}(R))\)

A	B
1	2
3	4

8.22.2. Aggregation

■ Aggregation fasst Werte einer Spalte zusammen.
□ Operation auf einer Menge oder Multimenge atomarer Werte (nicht Tupel)
□ Null-Werte gehen idR nicht mit ein
□ Summe (SUM)
□ Durchschnitt (AVG)
– Auch: STDDEV und VARIANCE
□ Minimum (MIN) und Maximum (MAX)
– Lexikographisch für nicht-numerische Werte
□ Anzahl (COUNT)
– Doppelte Werte gehen auch doppelt ein.
– Angewandt auf ein beliebiges Attribut ergibt dies die Anzahl der Tupel in der Relation.
– Zeilen mit NULL-Werten werden idR mitgezählt.

\(R\)

A	B
1	2
3	4
1	2
1	2

SUM(B) = 10
AVG(A) = 1,5
MIN(A) = 1
MAX(B) = 4
COUNT(A) = 4
COUNT(B) = 4

8.22.3. Aggregation – Beispiele

Film

Titel	Jahr	Länge	Typ	StudioName
Total Recall	1990	113	Farbe	Fox
Basic Instinct	1992	127	Farbe	Disney
Dead Man	1995	90	s/w	Paramount

■ MAX(Jahr): Jüngster Film
■ MIN(Länge): Kürzester Film
■ SUM(Länge): Summe der Filmminuten
■ AVG(Länge): Durchschnittliche Filmlänge
■ MIN(Titel): Alphabetisch erster Film
■ COUNT(Titel): Anzahl Filme
■ COUNT(StudioName): Anzahl Filme
■ AVG(SchauspName): syntax error

8.22.4. Gruppierung

■ Partitionierung der Tupel einer Relation gemäß ihrer Werte in einem oder mehr Attributen.
□ Hauptzweck: Aggregation auf Teilen einer Relation (Gruppen)
□ Gegeben
– Film(Titel, Jahr, Länge, inFarbe, StudioName, ProduzentID)
□ Gesucht: Gesamtminuten pro Studio
– Gesamtminuten(StudioName, SummeMinuten)
□ Verfahren:
– Gruppiere nach StudioName
– Summiere in jeder Gruppe die Länge der Filme
– Gebe Paare (Studioname, Summe) aus.

8.22.5. Gruppierung (group, \(\gamma\))

■ \(\gamma_L\)® wobei L eine Menge von Attributen ist. Ein Element in L ist entweder

1. Ein Gruppierungsattribut nach dem gruppiert wird
   

2. Oder ein Aggregationsoperator auf ein Attribut von R (inkl. Neuen Namen für das aggregierte Attribut)
   ■ Ergebnis wird wie folgt konstruiert:
   □ Partitioniere R in Gruppen, wobei jede Gruppe gleiche Werte im Gruppierungsattribut hat
   – Falls kein Gruppierungsattribut angegeben: Ganz R ist die Gruppe
   □ Für jede Gruppe erzeuge ein Tupel mit
   – Wert der Gruppierungsattribute
   – Aggregierte Werte über alle Tupel der Gruppe

8.22.6. Gruppierung – Beispiele

Film

Titel	Jahr	Länge	Typ	StudioName
Total Recall	1990	113	Farbe	Fox
Basic Instinct	1992	127	Farbe	Disney
Dead Man	1995	90	s/w	Paramount

■ Durchschnittliche Filmlänge pro Studio
□ \(\gamma_{Studio, AVG(Länge)→Durchschnittslänge}\)(Film)

■ Anzahl der Filme pro Schauspieler
□ \(\gamma_{SchauspName, Count(Titel)→Filmanzahl}\)(Film)

■ Durchschnittliche Anzahl der Filme pro Schauspieler
□ \(\gamma_{AVG(Filmanzahl)}(\gamma_{SchauspName, Count(Titel)→Filmanzahl}\)(Film))

■ Zu Hause:
□ Anzahl Schauspieler pro Film
□ Durchschnittliche Anzahl der Schauspieler pro Film
□ Studiogründung: Kleinstes Jahr pro Studio


■ Gegeben: SpieltIn(Titel, Jahr, SchauspName)
■ Gesucht: Für jeden Schauspieler, der in mindestens 3 Filmen spielte, das Jahr des ersten Filmes.
■ Idee
□ Gruppierung nach SchauspName
□ Bilde
– Minimum vom Jahr
– Count von Titeln
□ Selektion nach Anzahl der Filme
□ Projektion auf Schauspielername und Jahr
■ \(\pi_{SchauspName, MinJahr}(\sigma_{AnzahlTitel≥3}(\gamma_{SchauspName, MIN(Jahr)→MinJahr, COUNT(Titel)→AnzahlTitel}(SpieltIn)))\)


■ Gegeben: SpieltIn(Titel, Jahr, SchauspName) ■ Gesucht: Für jeden Schauspieler, der in mindestens 3 Filmen spielte, das Jahr des ersten Filmes und den Titel dieses Films. □ Genauer: Ein Titel des Schauspielers in dem Jahr ■ Idee □ Wie zuvor □ Anschließend Self-Join um Filmtitel zu bekommen. □ Anschließend Gruppierung nach SchauspName um Gruppe auf einen Film zu reduzieren. ■ \(\gamma_{SchauspName, MIN(MinJahr)→MinJahr, MIN(Titel)→Titel}( (SpieltIn) ⋈_{SchauspName = SchauspName, MinJahr = Jahr} (\pi_{SchauspName, MinJahr}(\sigma_{AnzahlTitel≥3}( \gamma_{SchauspName, MIN(Jahr)→MinJahr, COUNT(Titel)→AnzahlTitel}(SpieltIn) ) ) ) )\)

8.22.7. Komplexe Ausdrücke – Beispiele

■ Stud(Matrikel, Name, Semester)
■ Prof(ProfName, Fachgebiet, GebJahr)
■ VL(VL_ID, Titel, Saal)
■ Lehrt(ProfName, VL_ID)
■ Hört(Matrikel,VL_ID)
■ Gesucht: Fachgebiete von Professoren, die VL geben, die weniger als drei Hörer haben.
■ $\gamma_{Fachgebiet}$( (Prof ⋈ Lehrt) ⋈ ($\sigma_{ COUNT < 3(gVL_ID,COUNT(Matrikel)-> COUNT}$(Hört)) )
■ $\pi_{Fachgebiet}$( (Prof ⋈ Lehrt) ⋈ ($\sigma_{ COUNT < 3(gVL_ID,COUNT(Matrikel)-> COUNT}$(Hört)) )

8.22.8. Sortierung (sort, \(\tau\))

■ $\tau_L$(R) wobei L eine Attributliste aus R ist.
□ Falls L = (A1,A2,…,An) wird zuerst nach A1, bei gleichen A1 nach A2 usw. sortiert.

■ Wichtig: Ergebnis der Sortierung ist keine Menge, sondern eine Liste.
□ Deshalb: Sortierung ist letzter Operator eines Ausdrucks. Ansonsten würden wieder Mengen entstehen und die Sortierung wäre verloren.
□ Trotzdem: In DBMS macht es manchmal auch Sinn zwischendurch zu sortieren.

8.22.9. Semi-Join (⋊)

■ Formal
□ R(A), S(B)
□ R ⋉ S : = $\pi_A$(R⋈S)
= $\pi_A$(R) ⋈$\pi_{A\cap B}$(S)
= R⋈$\pi_{A\cap B}$(S)
□ In Worten: Join über R und S, aber nur die Attribute von R sind interessant.
□ Definition analog für Theta-Join
■ Nicht kommutativ: R ⋉ S ≠ S ⋉ R

8.22.10. Semi-Join

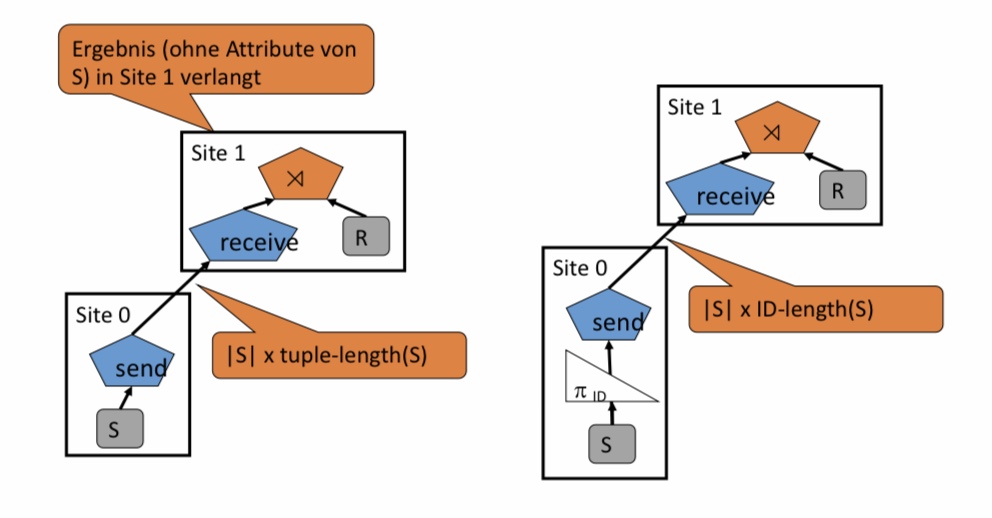
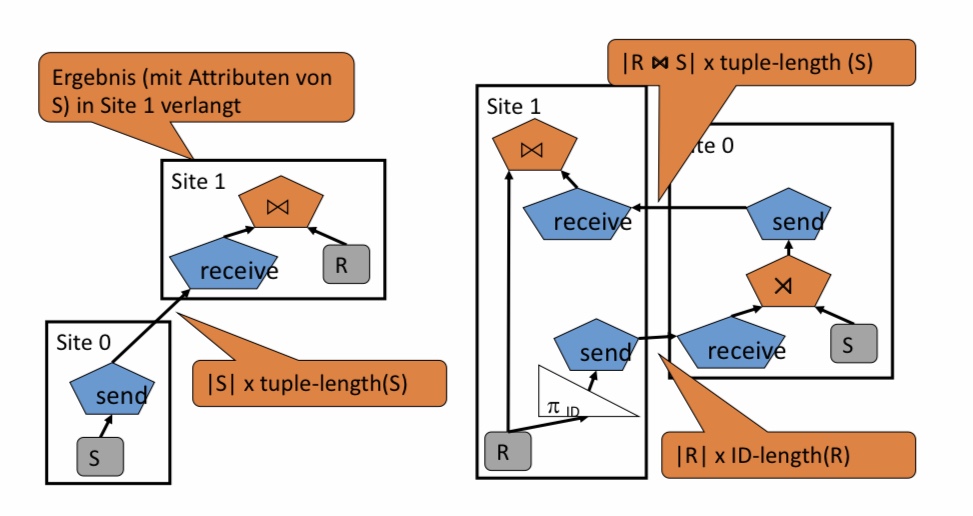
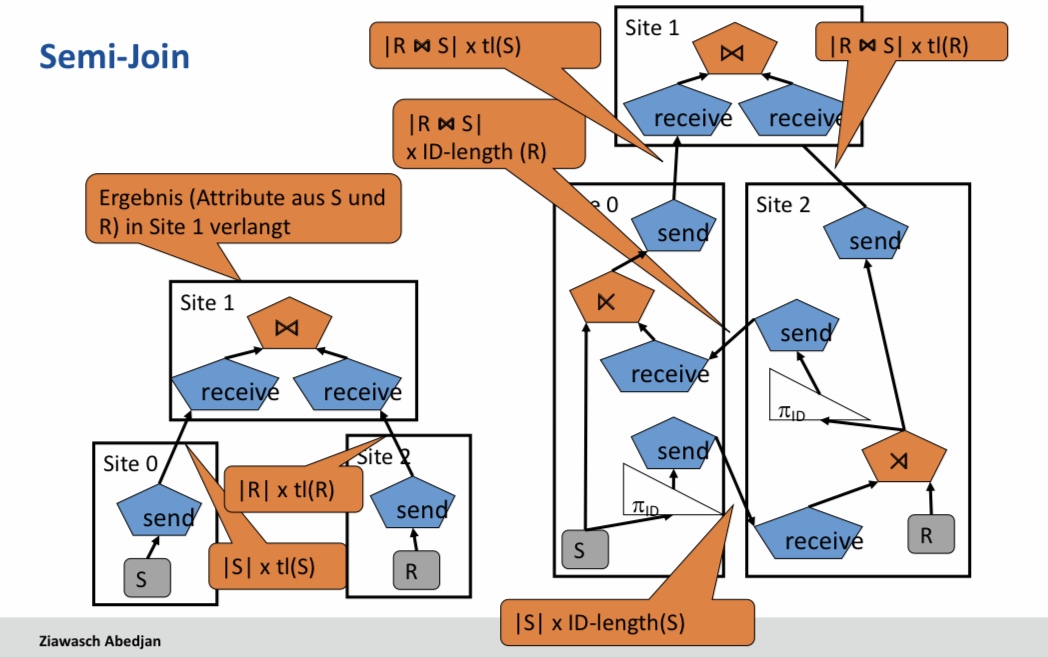
8.22.11. Outer Joins (Äußere Verbünde, |⋈|)

Übernahme von „dangling tuples“ in das Ergebnis und Auffüllen mit Nullwerten (padding)
Nullwert: $\perp$ bzw. null (≠ 0)

Full outer join
Übernimmt alle Tupel beider Operanden R |⋈| S

Left outer join (right outer join)
Übernimmt alle Tupel des linken (rechten) Operanden
R |⋈ S (bzw. R ⋈| S)

Herkömmlicher Join auch „Inner join“


R⋈S
R |⋈ S
R ⋈| S
R |⋈| S

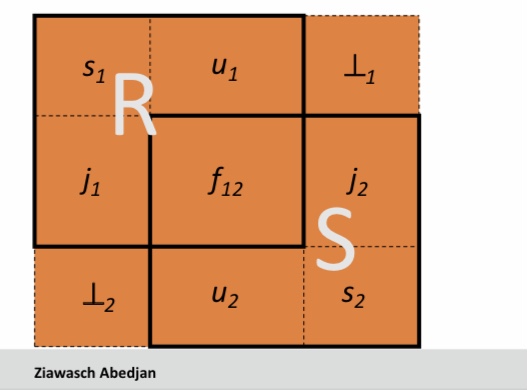
8.22.12. Outer Union (⊎)

■ Wie Vereinigung, aber auch mit inkompatiblen Schemata
□ Schema ist Vereinigung der Attributmengen
□ Fehlende Werte werden mit Nullwerten ergänzt

\(R\)

A	B	C
1	2	3
6	7	8
9	7	8

\(S\)

B	C	D
2	5	6
2	3	5
7	8	10

\(R⊎S\)

A	B	C	D
1	2	3	\(\perp\)
6	7	8	\(\perp\)
9	7	8	\(\perp\)
\(\perp\)	2	5	6
\(\perp\)	2	3	5
\(\perp\)	7	8	10

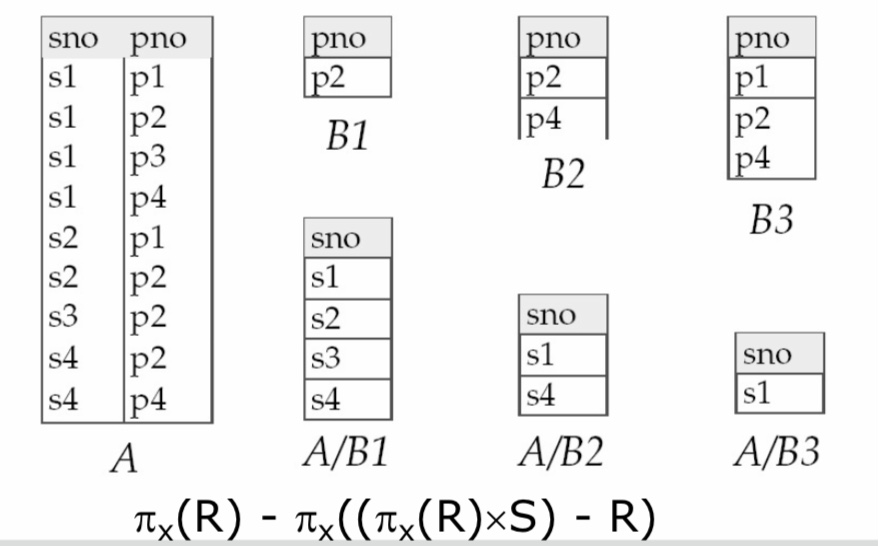
8.22.13. Division (division, /)

■ Typischerweise nicht als primitiver Operator unterstützt.
■ Finde alle Segler, die alle Segelboote reserviert haben.
■ Relation R(x,y), Relation S(y)
□ R/S = { t $\in$ R(x) | $\forall$ y $\in$ S $\exists$ $\in$ R}
□ R/S enthält alle x-Tupel (Segler), so dass es für jedes y-Tupel (Boot) in S ein xy-Tupel in R gibt.
□ Andersherum: Falls die Menge der y-Werte (Boote), die mit einem x-Wert (Segler) assoziiert sind, alle y-Werte in S enthält, so ist der x-Wert in R/S.
■ Hole die Namen von Angestellten, die an allen Projekten arbeiten.
□ Sinnvoller: Hole die Namen von Angestellten, die an allen Projekten arbeiten, in denen auch „Thomas Müller“ arbeitet.

8.22.14. Division – Beispiel

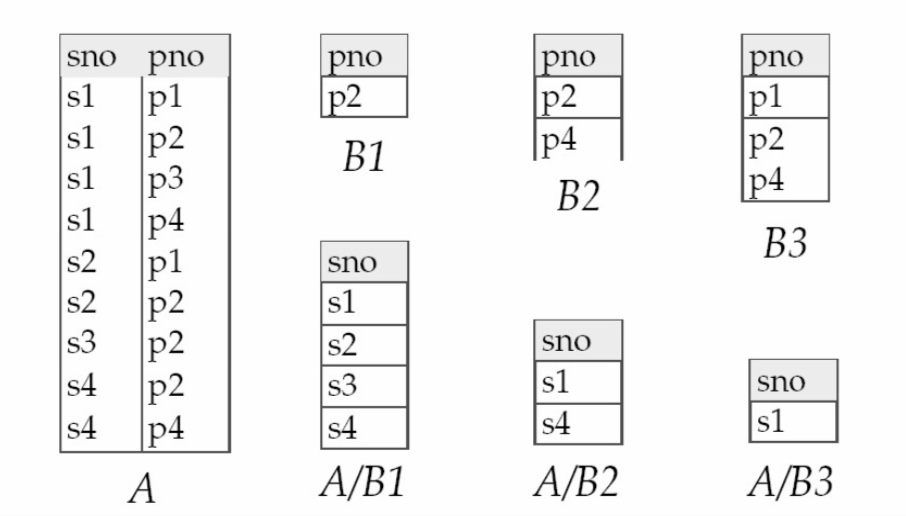
8.22.15. Division ausdrücken

■ Division ist kein essentieller Operator, nur nützliche Abkürzung.
□ Ebenso wie Joins, aber Joins sind so üblich, dass Systeme sie speziell unterstützen.

■ Idee: Um R/S zu berechnen, berechne alle x-Werte, die nicht durch einen y-Wert in S „disqualifiziert“ werden.
– x-Wert ist disqualifiziert, falls man durch Anfügen eines y-Wertes ein xy-Tupel erhält, das nicht in R ist.
□ Disqualifizierte x-Werte: $\pi_{x}$ (($\pi_{x}$(R) $\times$ S) − R)
□ R/S: $\pi_{x}$(R) − alle disqualifizierten Tupel

8.22.16. Division