11. Transaktionsmanagement#

title

Motivation - Transaktionsmanagement

■ Annahmen bisher
□ Isolation: Nur ein Nutzer greift auf die Datenbank zu
– Lesend
– Schreibend
□ In Wahrheit: Viele Nutzer und Anwendungen lesen und schreiben gleichzeitig.
□ Atomizität
– Anfragen und Updates bestehen aus einer einzigen, atomaren Aktion. DBMS können nicht mitten in dieser Aktion ausfallen.
– In Wahrheit: Auch einfache Anfragen bestehen oft aus mehreren Teilschritten.

Motivierendes Beispiel

Kontostand: 500
Philipp	Sarah
	read(K,y)
read(K,x)
x:=x+200
write(x,K)
commit
	y:=y-100
	write(y,K)
	commit
Kontostand: 400

11.1. Transaktionen#

11.1.1. Die Transaktion#

Eine Transaktion ist eine Folge von Operationen (Aktionen), die die Datenbank von einem konsistenten Zustand in einen konsistenten (eventuell veränderten) Zustand überführt, wobei das ACID-Prinzip eingehalten werden muss.

11.1.2. Transaktionen – Historie#

■ In alten DBMS kein Formalismus über Transaktionen
□ Nur Tricks

■ Erster Formalismus in den 80ern
□ System R mit Jim Gray
□ Erste (ineffiziente) Implementierung
□ ACM Turing Award
– For seminal contributions to database and transaction processing research and technical leadership in system implementation from research prototypes to commercial products.

■ ARIES Project (IBM Research)
□ Algorithms for Recovery and Isolation Exploiting Semantics
□ Effiziente Implementierungen
□ C. Mohan

■ Transaktionen auch in verteilten Anwendungen und Services
title
title

11.1.3. ACID#

■ Atomicity (Atomarität)
□ Transaktion wird entweder ganz oder gar nicht ausgeführt.

■ Consistency (Konsistenz oder auch Integritätserhaltung)
□ Datenbank ist vor Beginn und nach Beendigung einer Transaktion jeweils in einem konsistenten Zustand.

■ Isolation (Isolation)
□ Transaktion, die auf einer Datenbank arbeitet, sollte den „Eindruck“ haben, dass sie allein auf dieser Datenbank arbeitet.

■ Durability (Dauerhaftigkeit / Persistenz)
□ Nach erfolgreichem Abschluss einer Transaktion muss das Ergebnis dieser Transaktion „dauerhaft“ in der Datenbank gespeichert werden.

11.1.4. Beispielszenarien#

■ Platzreservierung für Flüge gleichzeitig aus vielen Reisebüros
□ Platz könnte mehrfach verkauft werden, wenn mehrere Reisebüros den Platz als verfügbar identifizieren.

■ Überschneidende Konto-Operationen einer Bank
□ Beispiele später

■ Statistische Datenbankoperationen
□ Ergebnisse sind verfälscht, wenn während der Berechnung Daten geändert werden.

11.1.5. Beispiel – Serialisierbarkeit#

■ Fluege(Flugnummer, Datum, Sitz, besetzt)
■ chooseSeat() sucht nach freiem Platz und besetzt ihn gegebenenfalls

EXEC SQL BEGIN DECLARE SECTION;
    int flug;
    char date[10];
    char seat[3];
    int occ;
EXEC SQL END DECLARE SECTION;
void chooseSeat() {
/* Nutzer nach Flug, Datum und Sitz fragen */
    EXEC SQL SELECT besetzt INTO :occ FROM Fluege
        WHERE Flugnummer=:flug
        AND Datum=:date AND Sitz=:seat;
if(!occ) {
        EXEC SQL UPDATE Fluege SET besetzt=TRUE
    WHERE Flugnummer=:flight AND Datum=:date AND Sitz=:seat;
        }
    else …
}

->Embedded SQL

11.1.6. Beispiel – Serialisierbarkeit#

■ Problem: Funktion wird von mehreren Usern zugleich aufgerufen

Schedule
User 1 findet leeren Platz
	User 2 findet leeren Platz
User 1 besetzt Platz
	User 2 besetzt Platz

■ Beide User glauben den Platz reserviert zu haben.

■ Lösung gleich
□ Serielle Schedules
□ Serialisierbare Schedules

11.1.7. Beispiel - Atomizität#

■ Problem: Eine Transaktion kann Datenbank in inkonsistenten Zustand hinterlassen.
□ Softwarefehler / Hardwarefehler

EXEC SQL BEGIN SECTION;
    int konto1, konto2;
    int kontostand;
    int betrag;
EXEC SQL END DECLARE SECTION;
void transfer() {
/* User nach Konto1, Konto2 und Betrag fragen */
    EXEC SQL SELECT Stand INTO :kontostand FROM Konten
        WHERE KontoNR=:konto1;
        If (kontostand >= betrag) {
    EXEC SQL UPDATE Konten
        SET Stand=Stand+:betrag
        WHERE KontoNR=:konto2;
    EXEC SQL UPDATE Konten
        SET Stand=Stand-:betrag
        WHERE KontoNR=:konto1;
    } else /* Fehlermeldung */
}

->Problem: Systemabsturz hier
->Lösung: Atomizität

11.1.8. Probleme im Mehrbenutzerbetrieb#

■ Abhängigkeiten von nicht freigegebenen Daten: Dirty Read

■ Inkonsistentes Lesen: Nonrepeatable Read

■ Berechnungen auf unvollständigen Daten: Phantom-Problem

■ Verlorengegangenes Ändern: Lost Update

11.1.9. Dirty Read#

T1	T2
read(A,x)
x:=x+100
write(x,A)
	read(A,x)
	read(B,y)
	y:=y+x
	write(y,B)
	commit
abort

Problem: T2 liest den veränderten A-Wert, diese Änderung ist aber nicht endgültig, sondern sogar ungültig.
Folie nach Kai-Uwe Sattler (TU Ilmenau)

11.1.10. Nonrepeatable Read#

■ Nicht-wiederholbares Lesen

■ Beispiel:
□ Zusicherung: x = A + B + C am Ende der Transaktion T1
□ x, y, z seien lokale Variablen

T1	T2
read(A,x)
	read(A,y)
	y:=y/2
	write(y,A)
	read(C,z)
	z:=z+y
	write(z,C)
	commit
read(B,y)
x:=x+y
read(C,z)
x:=x+z
commit

Problem: A hat sich im Laufe der Transaktion geändert.
x = A + B + C gilt nicht mehr
Beispiel nach Kai-Uwe Sattler (TU Ilmenau)

11.1.11. Das Phantom-Problem#

T1	T2
SELECT COUNT(*) INTO X FROM Mitarbeiter
	INSERT INTO Mitarbeiter VALUES (‚Meier‘, 50000, …)
	commit
UPDATE Mitarbeiter SET Gehalt = Gehalt +10000/X
commit

UPDATE Mitarbeiter SET Gehalt = Gehalt +10000/X commit Problem: Meier geht nicht in die Gehaltsberechnung ein. Meier ist das Phantom.
title
Beispiel nach Kai-Uwe Sattler (TU Ilmenau)

11.1.12. Lost Update#

T1	T2	A
read(A,x)		10
	read(A,x)	10
x:=x+1		10
	x:=x+1	10
write(x,A)		11
	write(x,A)	11

Problem: Die Erhöhung von T1 wird nicht berücksichtigt.
Folie nach Kai-Uwe Sattler (TU Ilmenau)

11.1.13. Transaktionen in SQL#

■ Idee: Gruppierung mehrerer Operationen / Anfragen in eine Transaktion
□ Ausführung atomar (per Definition)
□ Ausführung serialisierbar (per SQL Standard)
– Kann aufgeweicht werden (Isolationsstufen)

■ Ein SQL Befehl entspricht einer Transaktion
□ Ausgelöste TRIGGER werden ebenfalls innerhalb der Transaktion ausgeführt.

■ Beginn einer Transaktion: START TRANSACTION

■ Ende einer Transaktion (falls mit START TRANSACTION gestartet)
□ COMMIT signalisiert erfolgreiches Ende der Transaktion
□ ROLLBACK oder ABORT signalisiert Scheitern der Transaktion
– Erfolgte Änderungen werden rückgängig gemacht.
– Kann auch durch das DBMS ausgelöst werden: Anwendung muss entsprechende Fehlermeldung erkennen.

11.1.14. Isolationsebenen#

Aufweichung von ACID in SQL-92: Isolationsebenen

set transaction
[ { read only | read write }, ]
[isolation level {
    read uncommitted |
    read committed |
    repeatable read |
    serializable }, ]
[ diagnostics size ...]

■ Kann pro Transaktion angegeben werden

■ Standardeinstellung:

set transaction read write,
isolation level serializable

■ Andere Ebenen als Hilfestellung für das DBMS zur Effizienzsteigerung

11.1.15. Bedeutung der Isolationsebenen#

read uncommitted

□ Schwächste Stufe: Zugriff auf nicht geschriebene Daten
□ Falls man schreiben will: read write angeben (default ist hier ausnahmsweise read only)
□ Statistische und ähnliche Transaktionen (ungefährer Überblick, nicht korrekte Werte)
□ Keine Sperren: Effizient ausführbar, keine anderen Transaktionen werden behindert

read committed

□ Nur Lesen endgültig geschriebener Werte, aber nonrepeatable read möglich

repeatable read

□ Kein nonrepeatable read, aber Phantomproblem kann auftreten

serializable

□ Garantierte Serialisierbarkeit (default)
□ Transaktion sieht nur Änderungen, die zu Beginn der Transaktion committed waren (und eigene Änderungen).

11.1.16. Isolationsebenen – Übersicht#

Isolationsebene	Dirty Read	Nonrepeatable Read	Phantom Read	Lost Update
Read Uncommited	+	+	+	+
Read Committed	-	+	+	-
Repeatable Read	-	-	+	-
Serializable	-	-	-	-

11.2. Serialisierbarkeit#

11.2.1. Seriell vs. Parallel#

■ Grundannahme: Korrektheit
□ Jede Transaktion, isoliert ausgeführt auf einem konsistenten Zustand der Datenbank, hinterlässt die Datenbank wiederum in einem konsistenten Zustand.

■ Einfache Lösung aller obigen Probleme:
□ Alle Transaktionen seriell ausführen.

■ Aber: Parallele Ausführung bietet Effizienzvorteile
□ „Long-Transactions“ über mehrere Stunden hinweg
□ Cache ausnutzen

■ Deshalb: Korrekte parallele Pläne (Schedules) finden
□ Korrekt = Serialisierbar

11.2.2. Schedules#

Schritt	T1	T3
1.	Begin TA	Begin TA
2.	read(A,a1)	read(A,a2)
3.	a1 := a1 – 50	a2 := a2 – 100
4.	write(A,a1)	write(A,a2)
5.	read(B,b1)	read(B,b2)
6.	b1 := b1 + 50	b2 := b2 + 100
7.	write(B,b1)	write(B,b2)
8.	commit	commit

■ Ein Schedule ist eine geordnete Abfolge wichtiger Aktionen, die von einer oder mehreren Transaktionen durchgeführt werden.
□ Wichtige Aktionen: READ und WRITE eines Elements
□ „Ablaufplan“ für Transaktion, bestehend aus Abfolge von Transaktionsoperationen

11.2.2.1. Serialisierbarkeit#

■ Schedule
□ „Ablaufplan“ für Transaktionen, bestehend aus Abfolge von Transaktionsoperationen

■ Serieller Schedule
□ Schedule in dem Transaktionen hintereinander ausgeführt werden

■ Serialisierbarer Schedule
□ Es existiert ein serieller Schedule mit identischem Effekt.

11.2.2.2. Beispiel 1#

Serieller Schedule
Schritt	T1	T2
1.	BOT
2.	read(A)
3.	write(A)
4.	read(B)
5.	write(B)
6.	commit
7.		BOT
8.		read©
9.		write©
10.		read(A)
11.		write(A)
12.		commit

Serialisierbarer Schedule
Schritt	T1	T2
1.	BOT
2.	read(A)
3.		BOT
4.		read©
5.	write(A)
6.		write©
7.	read(B)
8.	write(B)
9.	commit
10.		read(A)
11.		write(A)
12.		commit

11.2.2.3. Beispiel 2#

Serialisierbar?
Schritt	T1	T3
1.	BOT
2.	read(A)
3.	write(A)
4.		BOT
5.		read(A)
6.		write(A)
7.		read(B)
8.		write(B)
9.		commit
10.	read(B)
11.	write(B)
12.	commit

11.2.2.4. Beispiel 3#

Aufgabe: Suche äquivalenten seriellen Schedule.

Schritt	T1	T3
1.	BOT
2.	read(A,a1)
3.	a1 := a1 – 50
4.	write(A,a1)
5.		BOT
6.		read(A,a2)
7.		a2 := a2 – 100
8.		write(A,a2)
9.		read(B,b2)
10.		b2 := b2 + 100
11.		write(B,b2)
12.		commit
13.	read(B,b1)
14.	b1 := b1 + 50
15.	write(B,b1)
16.	commit

Effekt: A = A − 150, B = B + 150

Schritt	T1	T3
1.	BOT
2.	read(A,a1)
3.	a1 := a1 – 50
4.	write(A,a1)
5.	read(B,b1)
6.	b1 := b1 + 50
7.	write(B,b1)
8.	commit
9.		BOT
10.		read(A,a2)
11.		a2 := a2 – 100
12.		write(A,a2)
13.		read(B,b2)
14.		b2 := b2 + 100
15.		write(B,b2)
16.		commit

Effekt: A = A − 150, B = B + 150

11.2.2.5. Beispiel 4#

Schritt	T1	T3	A	B
1.	BOT		100	100
2.	read(A,a1)
3.	a1 := a1 – 50		50
4.	write(A,a1)
5.		BOT
6.		read(A,a2)
7.		a2 := a2 * 1.03	51,5
8.		write(A,a2)
9.		read(B,b2)
10.		b2 := b2 * 1.03		103
11.		write(B,b2)
12.		commit
13.	read(B,b1)
14.	b1 := b1 + 50			153
15.	write(B,b1)
16.	commit

Effekt: A = (A − 50) * 1.03
B = B * 1.03 + 50

Schritt	T1	T3	A	B
1.	BOT		100	100
2.	read(A,a1)
3.	a1 := a1 – 50		50
4.	write(A,a1)
5.	read(B,b1)
6.	b1 := b1 + 50			150
7.	write(B,b1)
8.	Commit
9.		BOT
10.		read(A,a2)
11.		a2 := a2 * 1.03	51,5
12.		write(A,a2)
13.		read(B,b2)
14.		b2 := b2 * 1.03		154,5
15.		write(B,b2)
16.		commit

Effekt: A = (A − 50) * 1.03
B = (B + 50) * 1.03

11.2.2.6. Beispiel 5#

Schritt	T1	T3	A	B
1.	BOT		100	100
2.	read(A,a1)
3.	a1 := a1 – 50		50
4.	write(A,a1)
5.		BOT
6.		read(A,a2)
7.		a2 := a2 * 1.03	51,5
8.		write(A,a2)
9.		read(B,b2)
10.		b2 := b2 * 1.03		103
11.		write(B,b2)
12.		commit
13.	read(B,b1)
14.	b1 := b1 + 50			153
15.	write(B,b1)
16.	commit

Effekt: A = (A − 50) * 1.03
B = B * 1.03 + 50

Schritt	T1	T3	A	B
1.		BOT	100	100
2.		read(A,a2)
3.		a2 := a2 * 1.03	103
4.		write(A,a2)
5.		read(B,b2)
6.		b2 := b2 * 1.03		103
7.		write(B,b2)
8.		commit
9.	BOT
10.	read(A,a1)
11.	a1 := a1 – 50		53
12.	write(A,a1)
13.	read(B,b1)
14.	b1 := b1 + 50			153
15.	write(B,b1)

Effekt: A = A * 1.03 − 50
B = B * 1.03 + 50

11.2.2.7. Schedules#

Schritt	T1	T3
1.	BOT
2.	read(A)
3.	write(A)
4.		BOT
5.		read(A)
6.		write(A)
7.		read(B)
8.		write(B)
9.		commit
10.	read(B)
11.	write(B)
12.	commit

Serialisierbar? Nein,denn Effekt entspricht weder dem seriellen Schedule T1T3 noch dem seriellen Schedule T3T1

Serialisierbar? Nein, obwohl es konkrete Beispiele solcher Transaktionen gibt, für die es einen äquivalenten seriellen Schedule gibt. Man nimmt immer das Schlimmste an.

11.2.2.8. Beispiel 9#

Nochmal die beiden seriellen Schedules. Ist Ihnen etwas aufgefallen?

Schritt	T1	T3	A	B
1.	BOT		100	100
2.	read(A,a1)
3.	a1 := a1 – 50		50
4.	write(A,a1)
5.		BOT
6.		read(A,a2)
7.		a2 := a2 * 1.03	51,5
8.		write(A,a2)
9.		read(B,b2)
10.		b2 := b2 * 1.03		103
11.		write(B,b2)
12.		commit
13.	read(B,b1)
14.	b1 := b1 + 50			153
15.	write(B,b1)
16.	commit

Schritt	T1	T3	A	B
1.	BOT		100	100
2.	read(A,a1)
3.	a1 := a1 – 50		50
4.	write(A,a1)
5.	read(B,b1)
6.	b1 := b1 + 50			150
7.	write(B,b1)
8.	Commit
9.		BOT
10.		read(A,a2)
11.		a2 := a2 * 1.03	51,5
12.		write(A,a2)
13.		read(B,b2)
14.		b2 := b2 * 1.03		154,5
15.		write(B,b2)
16.		commit

T1T3 ≠ T3T1
Ist das schlimm?

11.3. Konfliktserialisierbarkeit#

11.3.1. Konflikte#

■ Bedingung für Serialisierbarkeit: „Konfliktserialisierbarkeit“

■ Konfliktserialisierbarkeit wird von den meisten DBMS verlangt (und hergestellt)

■ Konflikt herrscht zwischen zwei Aktionen eines Schedules falls die Änderung ihrer Reihenfolge das Ergebnis verändern kann.
□ „Kann“ - nicht muss.

■ Neue Notation: Aktion ri(X) bzw. wi(X)
□ read bzw. write
□ TransaktionsID i
□ Datenbankelement X

■ Transaktion ist eine Sequenz solcher Aktionen
□ r1(A)w1(A)r1(B)w1(B)

■ Schedule einer Menge von Transaktionen ist eine Sequenz von Aktionen
□ Alle Aktionen aller Transaktionen müssen enthalten sein
□ Aktionen einer Transaktion erscheinen in gleicher Reihenfolge im Schedule

■ Gegeben Transaktionen Ti und Tk
□ ri(X) und rk(X) stehen nicht in Konflikt
□ ri(X) und wk(Y) stehen nicht in Konflikt (falls X ≠ Y)
□ wi(X) und rk(Y) stehen nicht in Konflikt (falls X ≠ Y)
□ wi(X) und wk(Y) stehen nicht in Konflikt (falls X ≠ Y)
□ ri(X) und wk(X) stehen in Konflikt
□ wi(X) und rk(X) stehen in Konflikt
□ wi(X) und wk(X) stehen in Konflikt
– „No coincidences“: Man nimmt immer das schlimmste an. Die konkrete Ausprägung der write-Operationen ist egal.

■ Zusammengefasst: Konflikt herrscht falls zwei Aktionen
□ das gleiche Datenbankelement betreffen,
□ und mindestens eine der beiden Aktionen ein write ist.

11.3.2. Konfliktserialisierbarkeit#

■ Idee: So lange nicht-konfligierende Aktionen tauschen bis aus einem Schedule ein serieller Schedule wird.
□ Falls das klappt, ist der Schedule serialisierbar.

■ Zwei Schedules S und S‘ heißen konfliktäquivalent, wenn die Reihenfolge aller Paare von konfligierenden Aktionen in beiden Schedules gleich ist.

■ Ein Schedule S ist genau dann konfliktserialisierbar, wenn S konfliktäquivalent zu einem seriellen Schedule ist.

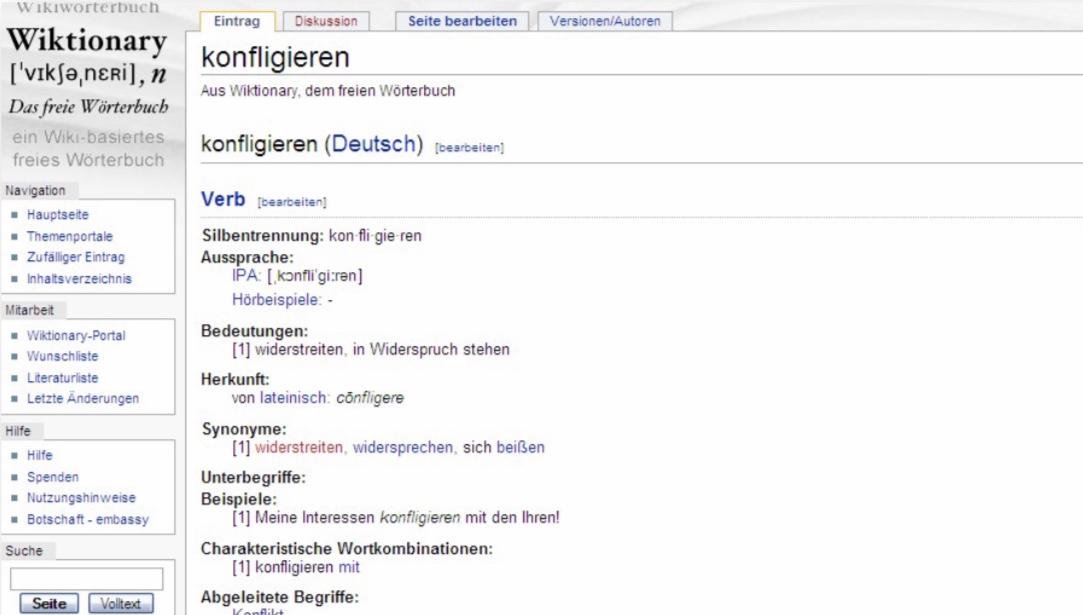
■ Schedule:
r1(A) w1(A) r2(A) w2(A) r2(B) w2(B) r1(B) w1(B)

■ Serieller Schedule T1T2:
r1(A) w1(A) r1(B) w1(B) r2(A) w2(A) r2(B) w2(B)

■ Serieller Schedule T2T1:
r2(A) w2(A) r2(B) w2(B) r1(A) w1(A) r1(B) w1(B)

11.3.2.1. Konflikt – konfligieren#

title

11.3.2.2. Konfliktserialisierbarkeit vs. Serialisierbarkeit#

■ Konfliktserialisierbarkeit => Serialisierbarkeit
□ Beispiel zuvor: Serialisierbarkeit war „zufällig“ aufgrund spezieller Ausprägungen der Aktionen möglich.
□ S1: w1(Y) w1(X) w2(Y) w2(X) w3(X)
– Ist seriell
□ S2: w1(Y) w2(Y) w2(X) w1(X) w3(X)
– Hat (zufällig) gleichen Effekt wie S1, ist also serialisierbar.
– Aber: Es müssten konfligierende Aktionen getauscht werden. Welche?
– S2 ist also nicht konfliktserialisierbar

■ Was fällt auf?
□ T3 überschreibt X sowieso -> Sichtserialisierbarkeit (nicht hier)

11.3.2.3. Graphbasierter Test#

■ Konfliktgraph G(S) = (V,E) von Schedule S:
□ Knotenmenge V enthält alle in S vorkommende Transaktionen.
□ Kantenmenge E enthält alle gerichteten Kanten zwischen zwei konfligierenden Transaktionen.
– Kantenrichtung entspricht zeitlichem Ablauf im Schedule.

■ Eigenschaften
□ S ist ein konfliktserialisierbarer Schedule gdw. der vorliegende Konfliktgraph ein azyklischer Graph ist.
□ Für jeden azyklischen Graphen G(S) lässt sich ein serieller Schedule S‘ konstruieren, so dass S konfliktäquivalent zu S‘ ist.
– D.h. S ist konfliktserialisierbar
– Z.B. topologisches Sortieren
□ Enthält der Graph Zyklen, ist der zugehörige Schedule nicht konfliktserialisierbar.

11.3.2.4. Schedules#

11.3.2.4.1. Beispiel 1#

Konfliktserialisierbar ?

Schritt	T1	T3
1.	BOT
2.	read(A)
3.	write(A)
4.		BOT
5.		read(A)
6.		write(A)
7.		read(B)
8.		write(B)
9.		commit
10.	read(B)
11.	write(B)
12.	commit

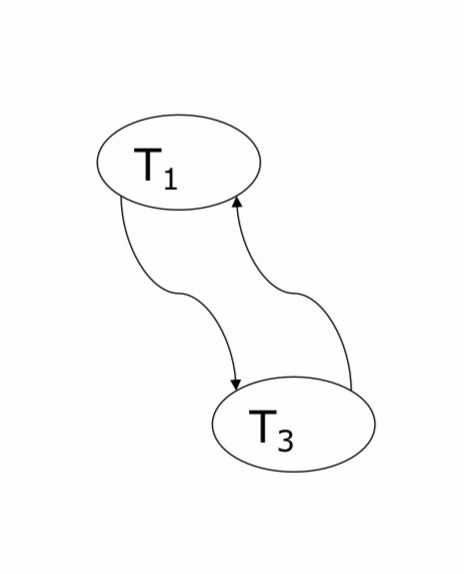
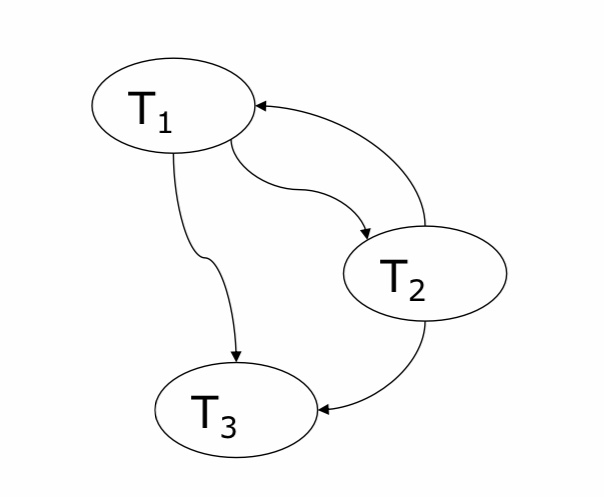
title

11.3.2.4.2. Beispiel 2#

title

Schritt	T1	T2	T3
1.	r(y)
2.			r(u)
3.		r(y)
4.	w(y)
5.	w(x)
6.		w(x)
7.		w(z)
8.			w(x)

S = r1(y) r3(u) r2(y) w1(y) w1(x) w2(x) w2(z) w3(x)

11.3.2.4.3. Beispiel 3#

Serialisierbarer Schedule

Schritt	T1	T2
1.	BOT
2.	read(A)
3.		BOT
4.		read©
5.	write(A)
6.		write©
7.	read(B)
8.	write(B)
9.	commit
10.		read(A)
11.		write(A)
12.		commit

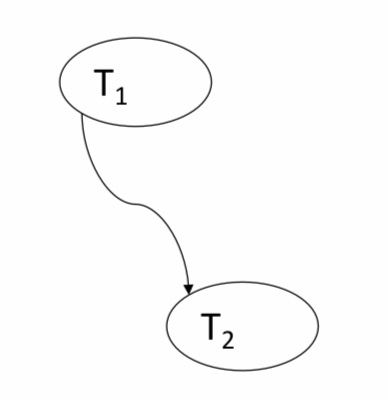
title

11.3.2.5. Beweis#

Konfliktgraph ist zykelfrei <=> Schedule ist konfliktserialisierbar
Konfliktgraph ist zykelfrei <=> Schedule ist konfliktserialisierbar
Leicht: Konfliktgraph hat Zykel => Schedule ist nicht konfliktserialisierbar
Bzw. Gegenbeispiel: T1 -> T2 -> … -> Tn -> T1
Konfliktgraph ist zykelfrei Þ Schedule ist konfliktserialisierbar
Induktion über Anzahl der Transaktionen n
n = 1: Graph und Schedule haben nur eine Transaktion.
n = n + 1:
Graph ist zykelfrei
=> ∃ mindestens ein Knoten Ti ohne eingehende Kante.
=> ∄ Aktion einer anderen Transaktion, die vor einer Aktion in Ti ausgeführt wird und mit dieser Aktion in Konflikt steht.
Alle Aktionen aus Ti können an den Anfang bewegt werden (Reihenfolge innerhalb Ti bleibt erhalten).
Restgraph ist wieder azyklisch (Entfernung von Kanten aus einem azyklischen Graph kann ihn nicht zyklisch machen).
Restgraph hat n-1 Transaktionen

11.4. Sperrkontrolle#

11.4.1. Scheduler#

■ Der Scheduler in einem DBMS garantiert konfliktserialisierbare (also auch serialisierbare) Schedules bei gleichzeitig laufenden Transaktionen.
□ Komplizierte Variante: Graphbasierter Test
– Inkrementell?
□ Einfachere Variante: Sperren und Sperrprotokolle
– In fast allen DBMS realisiert
□ Idee: Transaktion sperrt Objekte der Datenbank für die Dauer der Bearbeitung
– Andere Transaktionen können nicht auf gesperrte Objekte zugreifen.
BILD

11.4.2. Sperren#

Idee: Transaktionen müssen zusätzlich zu den Aktionen auch Sperren anfordern und freigeben.
Bedingungen
Konsistenz einer Transaktion
Lesen oder Schreiben eines Objektes nur nachdem Sperre angefordert wurde und bevor die Sperre wieder freigegeben wurde.
Nach dem Sperren eines Objektes muss später dessen Freigabe erfolgen.
Legalität des Schedules
Zwei Transaktionen dürfen nicht gleichzeitig das gleiche Objekt sperren.
Zwei neue Aktionen
li(X): Transaktion i fordert Sperre für X an (lock).
ui(X): Transaktion i gibt Sperre auf X frei (unlock).
Konsistenz: Vor jedem ri(X) oder wi(X) kommt ein li(X) (mit keinem ui(X) dazwischen) und ein ui(X) danach.
Legalität: Zwischen li(X) und lk(X) kommt immer ein ui(X)

11.4.3. Schedules mit Sperren#

■ Zwei Transaktionen
□ r1(A)w1(A)r1(B)w1(B)
□ r2(A)w2(A)r2(B)w2(B)

■ Zwei Transaktionen mit Sperren
□ l1(A)r1(A)w1(A)u1(A)l1(B)r1(B)w1(B)u1(B)
□ l2(A)r2(A)w2(A)

■ Schedule

T1	T2
l1(A)r1(A)w1(A)u1(A)
	l2(A)r2(A)w2(A)u2(A)
	l2(B)r2(B)w2(B)u2(B)
l1(B)r1(B)w1(B)u1(B)

□ Legal?
□ Konfliktserialisierbar?

T1	T3	A	B
		25	25
l(A); read(A,a1)
a1 := a1 + 100		125
write(A,a1); u(A)
	l(A); read(A,a2)
	a2 := a2 * 2	250
	write(A,a2); u(A)
	l(B); read(B,b2)
	b2 := b2 * 2		50
	write(B,b2); u(B)
l(B); read(B,b1)
b1 := b1 + 100		150
write(B,b1); u(B)

Legal? Serialisierbar? Konfliktserialisierbar?

11.4.4. Freigabe durch Scheduler#

■ Scheduler speichert Sperrinformation in Sperrtabelle
□ Sperren(Element, Transaktion)
□ Anfragen, INSERT, DELETE
□ Vergabe von Sperren nur wenn keine andere Sperre existiert
□ Alte Transaktionen
– l1(A)r1(A)w1(A)u1(A)l1(B)r1(B)w1(B)u1(B)
– l2(A)r2(A)w2(A)u2(A)l2(B)r2(B)w2(B)u2(B)
□ Neue Transaktionen
– l1(A)r1(A)w1(A)l1(B)u1(A)r1(B)w1(B)u1(B)
– l2(A)r2(A)w2(A)l2(B)u2(A)r2(B)w2(B)u2(B)
– Konsistent?

11.4.5. Schedules mit Sperren#

T1	T3	A	B
		25	25
l(A); read(A,a1)
a1 := a1 + 100		125
write(A,a1); l(B); u(A)
	l(A); read(A,a2)
	a2 := a2 * 2	250
	write(A,a2);
	l(B); abgelehnt!
read(B,b1)
b1 := b1 + 100			125
write(B,b1); u(B)
	l(B); u(A); read(B,b2)
	b2 := b2 * 2		250
	write(B,b2); u(B)

Legal? Serialisierbar? Konfliktserialisierbar? Zufall?

11.4.6. 2-Phasen Sperrprotokoll#

■ 2-Phase-Locking (2PL): Einfache Bedingung an Transaktionen garantiert Konfliktserialisierbarkeit.
□ Alle Sperranforderungen geschehen vor allen Sperrfreigaben
□ Die Phasen
– Phase 1: Sperrphase
– Phase 2: Freigabephase
□ Wichtig: Bedingung an Transaktionen, nicht an Schedule

11.4.6.1. 2-Phasen Sperrprotokoll – Beispiel#

T1	T3	A	B
		25	25
l(A); read(A,a1)
a1 := a1 + 100		125
write(A,a1); u(A)
	l(A); read(A,a2)
	a2 := a2 * 2	250
	write(A,a2); u(A)
	l(B); read(B,b2)
	b2 := b2 * 2		50
	write(B,b2); u(B)
l(B); read(B,b1)
b1 := b1 + 100		150
write(B,b1); u(B)

T1	T3	A	B
		25	25
l(A); read(A,a1)
a1 := a1 + 100		125
write(A,a1); l(B); u(A)
	l(A); read(A,a2)
	a2 := a2 * 2	250
	write(A,a2);
	l(B); abgelehnt!
read(B,b1)
b1 := b1 + 100			125
write(B,b1); u(B)
	l(B); u(A); read(B,b2)
	b2 := b2 * 2		250
	write(B,b2); u(B)

11.4.6.2. Deadlocks unter 2PL möglich#

■ T1: l(A); r(A); A:=A+100; w(A); l(B); u(A); r(B); B:=B-100; w(B); u(B)
■ T4: l(B); r(B); B:=B2; w(B); l(A); u(B); r(A); A:=A2; w(A); u(A)

T1	T4	A	B
		25	25
l(A); read(A,a1)
	l(B); read(B,b2)
a1 := a1 + 100
	b2 := b2 * 2
write(A,a1)		125
	write(B,b2)		50
l(B) – abgelehnt
	l(A) – abgelehnt

■ Lösung 1: Timeouts
■ Lösung 2: „Waits-for“-Graph zur Vermeidung von deadlocks

11.4.6.3. 2PL – Intuition#

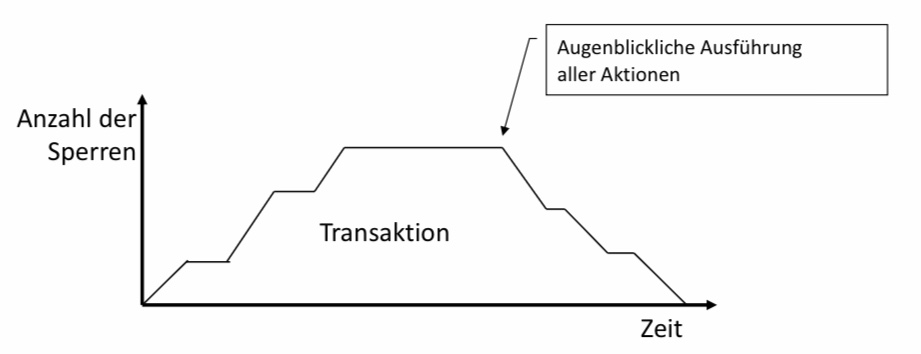
■ Jede Transaktion führt sämtliche Aktionen in dem Augenblick aus, zu dem das erste Objekt freigegeben wird.
■ Reihenfolge der Transaktionen des äquivalenten seriellen Schedules: Reihenfolge der ersten Freigaben von Sperren
title

11.4.6.4. 2PL – Beweis#

■ Idee: Verfahren zur Konvertierung eines beliebigen, legalen Schedule S aus konsistenten, 2PL Transaktionen in einen konfliktäquivalenten seriellen Schedule

■ Induktion über Anzahl der Transaktionen n

■ n = 1: Schedule S ist bereits seriell

■ n = n + 1:
□ S enthalte Transaktionen T1, T2, …, Tn.
□ Sei Ti die Transaktion mit der ersten Freigabe ui(X).
□ Behauptung: Es ist möglich, alle Aktionen der Transaktion an den Anfang des Schedules zu bewegen, ohne konfligierende Aktionen zu passieren.
□ Angenommen es gibt eine Schreibaktion wi(Y), die man nicht verschieben kann:
– … wk(Y) … uk(Y) … li(Y) … wi(Y) …
□ Da Ti erste freigebenden Transaktion ist, gibt es ein ui(X) vor uk(Y):
– … wk(Y) … ui(X) … uk(Y) … li(Y) … wi(Y) …
□ Analog für eine Leseaktion ri(Y)
□ Ti ist nicht 2PL

11.5. Sperren#

11.5.1. Mehrere Sperrmodi#

■ Idee: Mehrere Arten von Sperren erhöhen die Flexibilität und verringern die Menge der abgewiesenen Sperren.
□ Sperren obwohl nur gelesen wird, ist übertrieben
– Gewisse Sperre ist dennoch nötig
– Aber: Mehrere Transaktionen sollen gleichzeitig lesen können.
□ Schreibsperre
– Exclusive lock: xli(X)
– Erlaubt das Lesen und Schreiben durch Transaktion Ti
– Sperrt Zugriff aller anderen Transaktionen
□ Lesesperre
– Shared lock: sli(X)
– Erlaubt das Lesen für Transaktion Ti
– Sperrt Schreibzugriff für alle anderen Transaktionen
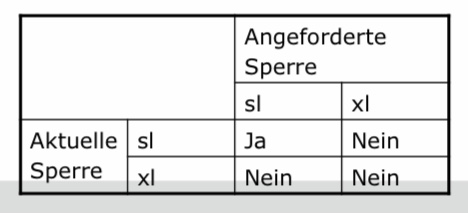
□ Kompatibilität
– Für ein Objekt darf es nur eine Schreibsperre oder mehrere Lesesperren geben.
□ Freigabe
– Unlock: ui(X) gibt alle Arten von Sperren frei

11.5.2. Bedingungen#

■ Konsistenz von Transaktionen
□ Schreiben ohne Schreibsperre ist nicht erlaubt.
□ Lesen ohne irgendeine Sperre ist nicht erlaubt.
□ Jede Sperre muss irgendwann freigegeben werden.

■ 2PL von Transaktionen
□ Wie zuvor: Nach der ersten Freigabe dürfen keine Sperren mehr angefordert werden.

■ Legalität von Schedules
□ Auf ein Objekt mit einer Schreibsperre darf es keine andere Sperre einer anderen Transaktion geben.
□ Auf ein Objekt kann es mehrere Lesesperren geben.
title

11.5.2.1. Beispiel#

■ T1: sl1(A)r1(A)xl1(B)r1(B)w1(B)u1(A)u1(B)
■ T2: sl2(A)r2(A)sl2(B)r2(B)u2(A)u2(B)
□ Konsistent?
□ 2PL?

T1	T2
sl(A); r(A)
	sl(A)r(A)
	sl(B)r(B)
xl(B) – abgelehnt!
	u(A)u(B)
xl(B)r(B)w(B)
u(A)u(B)

Legal? Konfliktserialisierbar? 2PL funktioniert auch hier!

11.5.3. Weitere Sperrarten#

■ Idee: Upgraden einer Sperre
□ Von Lesesperre zu Schreibsperre
□ Anstatt gleich strenge Schreibsperre zu setzen

■ Updatesperren
□ Erlaubt nur lesenden Zugriff
□ Kann aber Upgrade erfahren
□ Lesesperre kann dann keinen Upgrade erfahren

■ Inkrementsperre
□ Erlaubt lesenden Zugriff
□ Erlaubt schreibenden Zugriff falls Wert nur inkrementiert (oder dekrementiert) wird.
□ Inkremente sind kommutativ: Vertauschung ist erlaubt

Online-Skript Grundlagen der Datenbanksysteme

Transaktionsmanagement

Contents

11. Transaktionsmanagement#

11.1. Transaktionen#

11.1.1. Die Transaktion#

11.1.2. Transaktionen – Historie#

11.1.3. ACID#

11.1.4. Beispielszenarien#

11.1.5. Beispiel – Serialisierbarkeit#

11.1.6. Beispiel – Serialisierbarkeit#

11.1.7. Beispiel - Atomizität#

11.1.8. Probleme im Mehrbenutzerbetrieb#

11.1.9. Dirty Read#

11.1.10. Nonrepeatable Read#

11.1.11. Das Phantom-Problem#

11.1.12. Lost Update#

11.1.13. Transaktionen in SQL#

11.1.14. Isolationsebenen#

11.1.15. Bedeutung der Isolationsebenen#

11.1.16. Isolationsebenen – Übersicht#

11.2. Serialisierbarkeit#

11.2.1. Seriell vs. Parallel#

11.2.2. Schedules#

11.2.2.1. Serialisierbarkeit#

11.2.2.2. Beispiel 1#

11.2.2.3. Beispiel 2#

11.2.2.4. Beispiel 3#

11.2.2.5. Beispiel 4#

11.2.2.6. Beispiel 5#

11.2.2.7. Schedules#

11.2.2.8. Beispiel 9#

11.3. Konfliktserialisierbarkeit#

11.3.1. Konflikte#

11.3.2. Konfliktserialisierbarkeit#

11.3.2.1. Konflikt – konfligieren#

11.3.2.2. Konfliktserialisierbarkeit vs. Serialisierbarkeit#

11.3.2.3. Graphbasierter Test#

11.3.2.4. Schedules#

11.3.2.4.1. Beispiel 1#

11.3.2.4.2. Beispiel 2#

11.3.2.4.3. Beispiel 3#

11.3.2.5. Beweis#

11.4. Sperrkontrolle#

11.4.1. Scheduler#

11.4.2. Sperren#

11.4.3. Schedules mit Sperren#

11.4.4. Freigabe durch Scheduler#

11.4.5. Schedules mit Sperren#

11.4.6. 2-Phasen Sperrprotokoll#

11.4.6.1. 2-Phasen Sperrprotokoll – Beispiel#

11.4.6.2. Deadlocks unter 2PL möglich#

11.4.6.3. 2PL – Intuition#

11.4.6.4. 2PL – Beweis#

11.5. Sperren#

11.5.1. Mehrere Sperrmodi#

11.5.2. Bedingungen#

11.5.2.1. Beispiel#

11.5.3. Weitere Sperrarten#